Difractia luminii

Fenomenele de difractie desemneaza, în general, fenomene ondulatorii care se produc la propagarea luminii în medii cu neomogenitati suficient de mici astfel încât legile opticii geometrice nu mai sunt respectate.

Grimaldi (1665) observa prezenta luminii în umbra geometrica obtinuta pe ecranele opace  si interpreteaza fenomenul ca o dislocatie a fasciculului luminos.

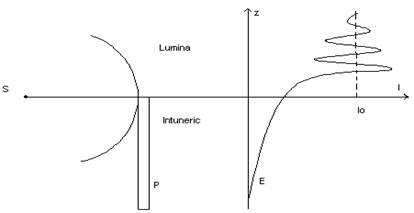
S - sursa punctiforma; (Σ) suprafata de unda; P-paravan opac;

 E- ecran; În partea dreapta a figurii se reprezinta dependenta

I(z) vizibila pe ecran.

Difractia poate fi definita si ca fenomenul de "ocolire" de catre lumina a obstacolelor atunci când dimensiunile acestora sunt comparabile cu lungimea de unda a radiatiilor incidente si implica modificarea repartitiei spatiale a intensitatii unei unde datorita obstacolelor (aperturi si/sau paravaneopace), modificare ce reprezinta franjele de difractie

 Umbra unei lame de ras

Problema fundamentala a difractiei consta în determinarea câmpului electromagnetic în orice punct din spatiu, atunci când sunt cunoscute pozitiile si formele surselor luminoase, paravanelor opace si aperturilor ce produc difractia. Riguros, aceasta înseamna rezolvarea ecuatiilor Maxwell pentru marimile de stare ale câmpului, cu conditii la limita corespunzatoare, dependente de natura si proprietatile optice ale ecranelor. Un astfel de deziderat reprezinta teoria vectoriala a difractiei si experienta arata ca este destul de greu de relizat. Exista un numar limitat de cazuri particulare în care problema poate fi rezolvata analitic cu considerarea caracterului vectorial si al starilor de polarizare. În unele conditii însa, se pot introduce o serie de ipoteze simplificatoare care conduc la situatii aproximative în buna concordanta cu datele experimentale. Astfel teoria scalara sau optica a difractiei elaborata sub doua 17317w228r forme: teoria Huygens-Fresnel si teoria Kirchhoff-Sommerfeldare la baza o serie de ipoteze care transforma problema vectoriala într-una scalara.

 Ipoteze ale studiului difractiei luminii în aproximatia optica

Dupa cum rezulta din experiente, fenomenele de difractie nu manifesta nici un efect sensibil de polarizare si, de asemenea, sunt independente de proprietatile materialelor ecranelor care le produc. Aceste doua constatari experimentale, împreuna cu observatia ca frecventele implicate sunt înalte, permit introducerea urmatoarelor ipoteze simplificatoare:

1° Unda electromagnetica vectoriala se înlocuieste cu o singura marime ondulatorie scalara complexa ce defineste perturbatia luminoasa functie de spatiu si timp, , si care se numeste amplitudine complexa. Amplitudinea complexa poate fi, de exemplu, una oricare dintre componentele rectangulare ale vectorilor  sau.

2° Informatia necesara pentru a preciza "starea luminii" într-un punct la un moment dat este continuta în expresia, aceasta marime specificând amplitudinea, faza si intensitatea luminii. În particular, intensitatea luminii este proportionala cu modulul patrat al amplitudinii complexe:

                                                                                            (10.1)

În aceste ipoteze, obtinerea unei solutii riguroase a problemei difractiei necesita rezolvarea ecuatiei de propagare a undelor:

                                                                          (10.2)

cu conditiile la limita corespunzatoare pe suprafata ecranelor (conditii care depind si de proprietatile optice ale materialelor). În ecuatia (10.2),  este indicele de refractie al mediului în care se propaga lumina.

3° Toate cazurile sunt reduse cu ajutorul analizei Fourier, la cazul undelor monocromatice, adica se considera:

                        .                                                               (10.3)

Substituind (10.3) în ecuatia de propagare a undelor (10.2) se obtine o ecuatie de tip Helmholtz, independenta de timp:

                                                                                               (10.4)

unde  este numarul de unda.

4° Urmeaza a se rezolva ecuatia Helmholtz (10.4) si se considera ca pe suprafata ecranelor pe care lumina se difracta:

                                                                                                      (10.5)

5° Toate sursele emit lumina într-un mediu izotrop si atunci amplitudinea complexa are numai o variatie radiala:

                         

astfel ca ecuatia (10.4) se scrie:

                                                                                                (10.6)